Prodigy. Thank you. As always I look forward to our meetings.

Mentor. At our last conversation, we talked about the accomplishments of that extraordinary people, the Ashkenazic Jews. We needed some data to continue. Were you able to find some?

Prodigy. A lot of not very useful stuff is out there, mostly accounts of Who's Who in Jewry. As you predicted, however, I was able to get what we needed from Arthur Hu. Hu's website is a veritable encyclopedia of ethnicity. Visiting it is an experience. He lists the percentage of Jews in 28 categories of achievement. It is apparent that the Jews represented in the data are mostly American, and consequently Ashkenazim. I brought the data for us to look at. It's in the form of a table.

Mentor. What do you make of the table? 

Prodigy. We already knew that Jews achieve far beyond their numbers, but with a mean IQ about one standard deviation higher than that of other Europeans, we expect high achievement from them.

Mentor. Can we bring something new ( if you'll forgive the expression) to the table, something novel, perhaps a new insight? Can we find a pattern in the data that will organize them in a meaningful way? Can we, for example, use the data to predict something new -- something yet to be observed -- a logical consequence of the pattern -- a prediction, verifiable, at least in principle?

Prodigy. You mean like the predicted existence of W and Z particles that grew out of the unified theory of weak and electromagnetic forces?

Mentor. An excellent example, though I had something less grand in mind. As you know Salam and Weinberg proposed W and Z in 1967, but not until 1983 were the particles observed. Incidentally, since Steven Weinberg won a Nobel Prize for the electroweak theory, he is no doubt represented in the percentage of Jewish Nobel laureates found in Hu's data. Do you think the same qualities that enable Jews to win Nobel prizes also equip them to hold top Hollywood positions?

Prodigy. The hallmark of the Ashkenazic Jew is intelligence. We know that intelligence correlates with many kinds of achievement, so it is not terribly surprising to find Jews disproportionately winning Nobel Prizes and also making movies.

Mentor. But surely some of the categories are more demanding of intellect than others. Which of them do you associate most closely with high IQ?

Prodigy. Well certainly not California Senators. Nobel Prize winners come immediately to mind, but also faculty at elite colleges, Ivy leaguers, Westinghouse winners, Supreme Court law clerks, MacArthur and ACM Turing Award winners. They all seem good bets for high IQs.

Mentor. Would you consider acceptance to the Ivy league and winning a Nobel Prize comparable intellectual feats?

Prodigy. Both groups are extremely bright. Based on SAT scores, Ivy Leaguers are far out on the right-hand tail of the bell curve. And keep in mind the Ivy League SAT scores are diluted by "legacy" admits, athletic scholarship winners, and minority affirmative action admissions.

Mentor. Why do you include Supreme Court law clerks?

Prodigy. They are mostly the best graduates of the best law schools. They have passed through a double screen, having survived a keen competition to be admitted to a premier law school, and then to have risen to the top of that group.
 

Prodigy. The MacArthurs are after all "genius" grants.

Mentor. Consider this. In 1999 there were 32 MacArthur winners. Fifteen were women. In the annals of human accomplishment, there is no precedent for that kind of female representation. Most of the recipients also have a distinctly left-wing flavor to their work. Others are positive flakes. Citations for the awards include phrases like "leader in the struggle for human rights in southern Africa," "scholar of race relations," "a strong socio-political sensibility in her works" etc. One of the 1995 geniuses, the feminist musicologist Susan McClary is described in the award announcement as "a musicologist who explores the relationship between human experiences and music and relates the creation of musical works to their social context." One of her major discoveries is that classical music is full of phallic themes. John Leo writing in U.S. News and World Report, observed "A lot of the [MacArthur] award winners are either ideologues . . . or low-luster laborers in the traditional vineyards of the left." I am afraid, Prodigy, that if you are looking for an antiseptic link to intelligence, the MacArthur grantees will not do.

Prodigy. OK so we'll scratch the "geniuses." I also have a problem with the Nobel laureates in the table. The Jews represented in the table are primarily American Jews, whereas the Nobel laureates come from all over. There is a certain incompatibility. We should be looking at American Jews there too, so with your permission I will substitute the percentage of American Nobelists who are Jewish. The number is 27 percent.

Mentor. Well, let's see what the table looks like after selecting the areas with the most obvious links to IQ.

Prodigy. The average in the six surviving categories is 27 percent Jewish, with a spread that looks like a thin film. I suggest a generalization: American Jews will constitute about 27 percent of any group whose distinguishing characteristic is intelligence. Can we call this Prodigy's conjecture?

Mentor. If you like, but I do have some questions.

Prodigy. Oops.

Mentor. As we continue out along the right tail of the bell curve, the highest IQ group will be increasingly represented. Since the faculty of elite colleges as well as supreme court clerks have a greater percentage of Jews (30) than the Nobel laureates (27), can we infer that these professors and law clerks are brighter on average than Nobel laureates?

Prodigy. The professors, law clerks and Nobel laureates are all so highly selected that distinguishing among them with respect to IQ is difficult. A more likely explanation is that in this context, 27 = 30.

Mentor. How about a prediction based on your conjecture?

Prodigy. Let me think for a moment. We know the percentage of Jews in the high IQ areas, i.e., 27%, and also their percentage in the general population. In addition, we know that the mean Jewish IQ is about one standard deviation above that of other European types. From this I will estimate the mean IQ of the Nobel laureates.

Mentor. And how exactly will you do that?

Prodigy. Let's define a few quantities: N_J is the number of Jews in the U.S.; N_E is the corresponding number of non-Jews of European ancestry; P is the normalized probability distribution (assumed Gaussian) of IQ among non-Jewish European types; λ is the IQ of the Nobelist with the lowest IQ, the bottom of his class so to speak; f_J is the fraction of Jews among the Nobelists, i.e., 0.27, which we also assume to be the fraction of Jews in the general population with IQ's at or above λ; finally, Δ is the difference in mean IQ (European - Jewish), i.e., -1.0. We may then write:

where in (1) we have used the following transformation: 

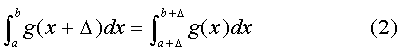Equation (1) is more conveniently written in terms of the ratio, N_J /N_E, i.e., 

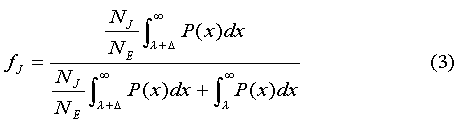Mentor, do you have census data handy so I can find the ratio N_J /N_E?

Mentor. According to 1994 U.S. Census Bureau estimates, Ashkenazic Jews numbered 5.88 million, and non-Hispanic whites 186.85 million, giving the ratio, N_J /N_E as 0.0315.
 

Mentor. What about their average IQ?

Prodigy. There are several averages we can compute, the average IQ of the Jewish Nobelists, the non-Jewish Nobelists, and all the Nobelists.

Mentor. Shouldn't they all be the same?

Prodigy. Not really. The Jewish Nobelists will have the highest average IQ, because as we move out along the right-hand tail of the distribution curves, on past the dimmest bulb threshold, the Jewish distribution becomes ever more dominant. Remember, at the threshold Jews are 1.60 standard deviation beyond their mean, while the non-Jews are 2.60 SD out from their mean.

We can compute the Jewish average, < IQ_J > as:

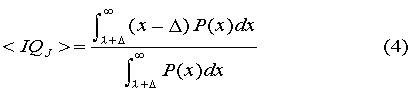The denominator in (4) re-normalizes the distribution for Jews. In the numerator we have used the transformation,

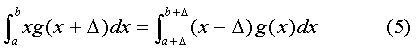Doing the arithmetic, we find: < IQ_J > = 3.02 or 145.3 IQ points. That is, to 3 figures we predict the average IQ of the Jewish laureates to be 145.

The average IQ of the non-Jewish Nobelists, < IQ_E >, is simply

Doing the arithmetic here gives: < IQ_E > = 2.91 or 143.7 IQ units. To 3 figures we estimate the average IQ of the non-Jewish laureates as 144, 1 point lower than that of the Jews. Sparing you the obvious arithmetic, we estimate the average IQ of the laureates overall to be 144.2 or simply 144, the same as the non-Jewish average.

Mentor. I asked earlier if professors at elite universities and Supreme Court law clerks are brighter than Nobel laureates since the Jewish presence is a bit greater in these areas, i.e., 30% vs. 27%. You answered to the effect that for our purposes, 27 = 30. What happens if you plug 30 percent into your engine instead of 27?

Prodigy. Just a moment while I do the computation . . . A 30 percent Jewish presence yields an overall average IQ of 146 instead of 144. Not a great difference would you say? It seems my 27 = 30 statement is more or less justified, a two point IQ difference being well within the error of my analysis, not to mention the state of the psychometric art.

Mentor. I must say I am impressed.

Prodigy. Do you recall a Problem for the Heterodox posed by La Griffe du Lion that asked for an estimate of the average IQ of the Nobel laureates? Do you think my solution will be satisfactory? Will I be eligible for a prize?

Mentor. You may be eligible for a prize. La Griffe has been known occasionally to award cigars, but that will have to wait until you grow up.