|
|
|
RACIAL DISPARITIES IN SCHOOL DISCIPLINE
The Bias Hunters In September 1999, six black high school students were expelled for brawling violently with other students at a Decatur, Ill. football game. Grabbing the spotlight, the Reverend Jesse Jackson made a house call. His presence in Decatur propelled a local event to the nation's front pages. Sleepy sociologists awoke to the call. One team of investigators from the Applied Research Center of Oakland interrupted a study to rush forward with preliminary results. They found that black students are suspended and expelled at disproportionate rates. "The figures are astounding," declared Rev. Jackson as he, the Oakland group and the press joined in mutual exploitation of the moment. A year later, in the December 2000 issue of La Griffe du Lion, we asked: Suppose a half-white, half-black school system suspends 1 percent of its students for disruptive behavior. What is the most probable racial makeup of the suspended group? The question began the section, "Games with Fuzzy Variables," but December's
game is June's analytical scalpel. With it we will peel back layers of misinformation
to reveal race and school discipline in a greater social context.

Figure 1. Aggressiveness distributions. The curves for blacks and whites are separated by a mean difference, Δ = 0.37 SD. Thresholds for suspension, assault and "serious assault" are designated λ1, λ2 and λ3, respectively.In general, schools (or school systems) have different tolerances for disagreeable behavior. Irrespective of where the boundaries of acceptable conduct are set, in the absence of bias, discipline rates should be consistent with the 0.37 SD aggressiveness gap. In Griffian terms, standards of tolerance correspond to points on the aggressiveness axis, beyond which punishment is triggered. By constraining the proportions of suspended (or expelled) students to be consistent with the 0.37 SD aggressiveness gap, we can predict how discipline rates should break down by race in the absence of racial discrimination. In brief, if NB and NW are the number of black and white students enrolled in a particular school system, and NS is the number students suspended (or expelled), then we may write: 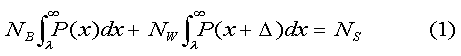
Close agreement between prediction and observation indicates that punishment was dispensed without prejudice. For diehard activists who require more proof, we develop additional criteria below. A Test for Bias When school discipline is administered in an evenhanded manner without regard to race, blacks will be punished out of proportion to their numbers. That is the expected norm. Disproportionate discipline therefore cannot serve as a criterion for racial bias. On the other hand, we cannot dismiss the possibility that bias (racial or otherwise) can creep into the discipline process. In fact, given the number of schools in the US and what we know of human nature, it would be a statistical miracle if it did not. In this regard, a test for bias would be useful. An existing test, known as the "ten percent rule," has been in use for years. It is employed by bias hunters to judge whether a racial group has been the victim of discrimination. The rule states that if a group's representation among the ranks of the punished exceeds its representation in the school population by more than 10 percent, the group has been unfairly punished. In the Skiba study African Americans made up 69 percent of those suspended and 56 percent of those enrolled. Because 69 exceeds 56 by 23 percent (comfortably more than 10 percent), the ten percent rule found blacks to be casualties of discrimination. There are two reasons why a rule like the ten percent rule does not work. 1) It is arbitrary, and 2) it is based on an ill-founded notion that all peoples are alike. We propose a test for bias that is neither arbitrary nor based on false assumptions. Like the 10 percent rule it looks at how the numbers of disciplined students break down by race, but the similarity ends there. The test can sniff out bias wherever it hides. And if it finds it, you can bet your last dollar it is there. We have seen how to predict the most probable numbers of students, black and white, who in the absence of bias will be suspended or expelled. The actual numbers will vary because of statistical fluctuations. Imagine a large (infinite) ensemble of school districts, each a replica of the Skiba district. Each has the same numbers of black and white students and applies the same criteria for meting out discipline. Within the ensemble students may be exchanged between districts, but always a black for a black or a white for a white. Because intra-ensemble exchange is allowed, the districts of the ensemble will have different numbers of suspended and expelled students. If we sample the districts in the ensemble, the central limit theorem assures us that we will find the numbers of suspended and expelled students distributed normally about their ensemble averages. We postulate that the ensemble averages are those predicted by (1). Thus, if n* is the predicted value of (say) suspended blacks, its standard error, σ, is given by
where again NS is the total number of suspended students. Absent bias, there is only a 5 percent chance that the observed number of suspended or expelled students from a group will fall outside 2 standard errors of n*. Thus, a test for bias may be constructed as follows:
In the Skiba example, n* = 1692, and the total number of suspended
students, NS = 2461, giving a standard error of 23.
The difference between the predicted and actual numbers of suspended blacks
is 0.17 σ. For expulsion, the difference is
0.48 σ. Plainly, bias was not a factor.
Recently, a remarkable paper appeared in the Journal of the American
Medical Association that bears upon this issue. The article, "Long-term
Effects of an Early Childhood Intervention on Educational Achievement and
Juvenile Arrest," A. J. Reynolds, J. A. Temple, D. L. Robertson and
E. A, Mann, JAMA, 285, 2339-2346 (2001), is a 15-year
follow-up of urban, mostly black, low-income children who matriculated
through an early intervention program in the Chicago public schools. The
authors describe impressive long-term gains made by the children. We put their data through the Griffian engine
and thus obtained an unexpected and extraordinary result.
Impressive achievements aside, there is more to these data than is immediately apparent. All six outcomes listed are for binary achievements. That is, a student either completes high school or doesn't, gets left back or doesn't. The two groups have different rates of success in each category. If we regard each item as a threshold for a fuzzy variable, the method of thresholds will reveal the fuzzy variable gap between the two groups in each category. Table 3 displays the calculated gaps. The result was unanticipated.
The gaps created by the early intervention program are almost
constant.
We are
probably looking not at six fuzzy variables,
but one! -- a unique human attribute that was modified by early intervention,
and whose change persisted through young adulthood. A
shift in the distribution of this variable by about 0.3 SD accounts
quantitatively for all the results of Table 2. We might call the
variable, "socialization," and its shift to higher values, "getting civilized." There is yet hope.
APPENDIX: The Method of Thresholds in Brief Let FB and FW be the fractions of black and white students, respectively, who are suspended by a given school. Let λ be the point on the aggressiveness axis beyond which suspension kicks in. That is, λ is the threshold for suspension. Its value will vary from school to school because tolerance for disagreeable behavior varies. We may write, 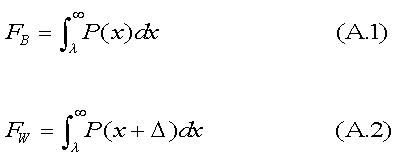
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||