|
|
|
AGGRESSIVENESS, CRIMINALITY AND SEX DRIVE BY RACE, GENDER AND ETHNICITY
"Who is a man that is not angry?"
--- Alcibiades to the Athenian Senators (Timon of Athens)
Most folks would agree that men tend to be more aggressive than women. We observe this in other mammals too.
Quantifying the difference, however, presents a problem. The variable, 'aggressiveness,' is fuzzy. It is not like height or
weight. We have no rulers or scales for it. Nevertheless, group differences in fuzzy variables can be precisely determined.
For this purpose, we introduce the method of thresholds, and illustrate its use by assessing the
aggressiveness gender difference.
Aggressiveness by Gender Several data sources list the proportions of men and women who commit assault in any given year. The best of these is the
National Crime Victimization Survey (NCVS) of the Justice Department. Each year it canvasses a representative sample of
about 80,000 Americans, from roughly 43,000 households. From the responses, a picture of crime emerges that does not
depend on apprehending criminals or even reporting crimes. The last full report of the NCVS, issued in 1994, lists the
number of single-victim assaults in the nation for that year, and the perceived sex of the offenders. From these data and
population estimates from the Census Bureau, we discover that 0.961 percent of women and 4.51 percent of men
perpetrated some kind of assault in the U.S. in 1994. Figure 1 shows male and female distributions for aggressiveness. We assume them to be normal. The assault threshold
shown in the figure has been placed to make the area to its right and under the male (red) distribution 4.51 percent of the
total. The female (blue) distribution has been displaced to make the area under it and to the right of the assault threshold
0.961 percent of the total. When these conditions are fulfilled, the resulting 'distance,' Δ, between the two distributions is
the mean gender difference for aggressiveness in standard deviation units (SD). A procedure for doing this analytically is
presented in Appendix A. Note, we neither defined the fuzzy variable nor created a scale for measuring it to obtain its
group difference. Using NCVS data in this way, the male - female mean
difference, Δ, is 0.65 SD. That is, men are more
aggressive than women by 0.65 SD. 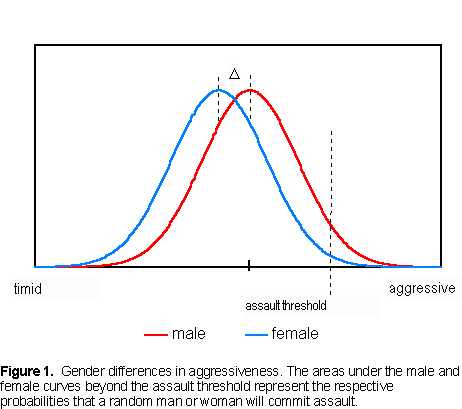 Aggressiveness by Race Turning to racial differences in aggressiveness, the NCVS is less useful because its racial categories are blurred by the absence of a classification for Hispanics. Hispanics exhibit different group behaviors from non-Hispanic whites and blacks, yet the NCVS tells us nothing about them. Both NCVS categories, black and white, include Hispanics. Most Hispanic Americans classify themselves as white. If victims are given a binary choice, they too will usually describe Hispanic assailants as white. That aside, we find from NCVS and census data that 2.20 percent of whites and 5.00 percent of blacks were perceived as assailants in 1994. Again, using assault as a threshold for aggressiveness, the method of thresholds finds that whites are less aggressive than blacks by 0.37 SD. To include Asians in our study, we turn to data gleaned from INTERPOL year books by J. Philippe Rushton (Society, Jan-Feb 1995). Rushton looked at 23 predominantly African countries, 41 Caucasian, and 12 Asian countries. Per 100,000 members of each group, he found 'serious assault' rates of 213, 63, and 27, respectively. Applied to these numbers, the method of thresholds yields a black - white mean difference for aggressiveness of 0.37 SD in perfect (if fortuitous) agreement with NCVS assault results, this despite that the INTERPOL threshold for serious assault is much higher than the NCVS standard. The white - Asian mean difference from these data is 0.24 SD. Of the three groups, Asians are the least aggressive, blacks the most. The 'distance' between blacks and whites is about 50 percent greater than between whites and Asians. Table 1 summarizes the results as Standard Aggressiveness Values.
Figure 2 presents the aggressiveness distributions for blacks, whites and Asians determined from the INTERPOL data. From them we see that the threshold for 'serious assault' is way out on all three curves (3.2 SD from the white mean). On this scale, most people in each of the three races will tend to be neither particularly timid nor aggressive. They mostly fall within one standard deviation of the white mean. 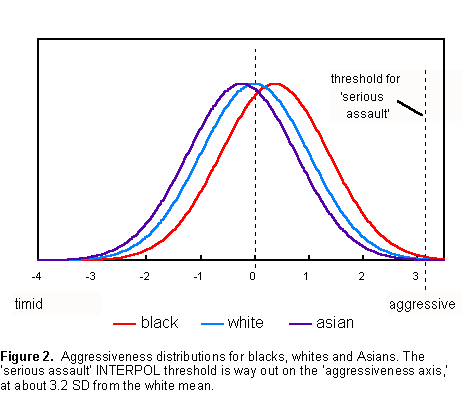
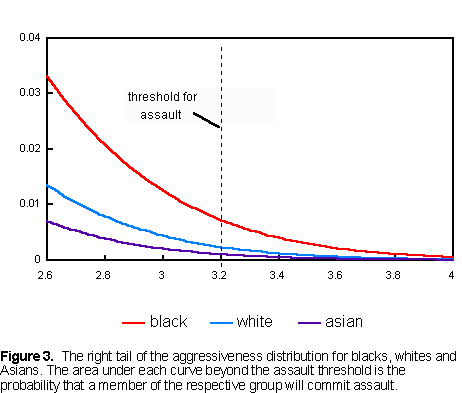 Criminality by Race, Gender and Hispanic Origin In this section we examine group differences in another fuzzy variable 'criminality.' Criminality refers to a degree of disaffection from society that leads to criminal behavior. It is a state of mind. No one is satisfied with every detail of the laws that constrain him, whether they be speed limits or tax laws. Near the bottom of the scale of criminality is the man who drives 10 mph above the speed limit. Near the top is the violent criminal. Most of us fall somewhere between the person who obeys every law and the one who delights in breaking them. Using Department of Justice data, we constructed a scale of Standard Criminality. On it we placed black males, blacks, Hispanic males, Hispanics, white males, whites, black females, Hispanic females and white females. As a non-fuzzy threshold for criminality we chose incarceration rate. Incarceration meets all our requirements. It is non-fuzzy, unambiguously related to criminality, and reliable data are available. The Department of Justice publication, Prisoners in 1998, lists incarceration rates for 1997. Most notably, it breaks out Hispanics from non-Hispanic whites and non-Hispanic blacks. Some data from this publication are reproduced in Table 2 along with quantities derived from them.
From the incarceration rates in Table 2, using the method of thresholds, we constructed a table of Standard Criminalities (Table 3).
The table of Standard Criminality values may be used to calculate the mean criminality difference between groups. For example, the mean difference between Hispanic males and white females is (0.430) - (-0.817) or 1.25 SD. Eyeballing the table shows that females of each group lag behind their male counterparts in criminality by about 1 SD, but black females fall only ~0.2 SD behind white males. We also investigated how mean differences in criminality vary with time. Time invariance would suggest that criminality is an inherent property of a group. Unfortunately, time series data from the Justice Department does not split out Hispanics from whites and blacks. Though corrupted in this way, these data can still be used to answer the time invariance question. In the decade spanning 1987 to 1997, incarceration rates almost doubled, but group criminality differences remained almost constant. Including Hispanics, the mean criminality differences between white and black males for the years 1987, 1992 and 1997 were 0.842 SD, 0.852 SD and 0.842 SD, respectively. Finally, if standard criminalities are characteristic of groups, they should also remain invariant across international boundaries. We looked at incarceration rates from the U.K. reported by the Home Office in its publication, Prison Statistics England and Wales 1995. According to the Home Office, 134 whites and 1049 blacks per 100,000 of each group were imprisoned. The method of thresholds crunched the U.K. data to yield a black-white mean criminality difference of 0.694 SD. This may be compared with the black-white difference of 0.736 SD for American blacks computed from standard criminalities in Table 3. The results strongly suggest the inherent character of criminality. Though U.S. incarceration rates for each group are significantly greater than those in the U.K., the black/white criminality differences are within 0.04 SD of each other. We have observed analogous occurrences in seemingly unrelated spheres. Math SAT scores, for example, increase linearly with family income for both blacks and whites, but the racial gap remains constant at about 1 SD.
From these data we constructed Standard Sex Drive values using the method of thresholds. They are presented in Table 5.
Games with Fuzzy Variables If aggressiveness triggers the behavior that results in suspension, we can answer this question by consulting the table of Standard Aggressiveness values, where we find that whites lag behind blacks by 0.37 SD. We infer from this that the most probable racial makeup of suspended students is 73 percent black. In Appendix B, we develop machinery using standard fuzzy variables to crunch this result, and others.
Let f be the fraction of the reference group reaching or surpassing some threshold value, λ, of the fuzzy variable. The quantities, λ and f are related as follows:
The fraction, fB , of group B reaching or surpassing λ is: 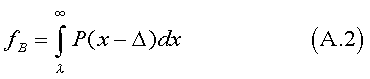
Knowing the fraction, f, (A.1) may be used to obtain a value for the threshold, λ, in standard units. With this threshold in hand and the value of fB , (A.2) yields Δ, the standard value of x. The tables of standard values found in the body of this essay were produced in this way, taking P to be Gaussian,
In general, suppose NS slots are to be filled in rank order on some property from a pool made up of N1 members of Group 1,
N2 members of Group 2, etc. Members of all groups will be selected to fill a slot if they have a property value equal to or
greater than some threshold, . The threshold, λ, is the value of the property exhibited by the last person to fill a slot. It is
determined by the pool sizes, the number of slots available and the property distributions for each group. The variables are
related as follows: where Pi is the normalized distribution function of the property for group i. We have assumed previously that Pi (x) = P(x - Δi), where P is the distribution for a group designated as the reference group. Accordingly, Equation B.1 may be written as:
The displacement, Δi , is the standard value of the property for Group i. Each term on the left side of (B.2) represents the number of members from the corresponding group who fill slots. The terms sum to the number of slots, NS. From the pool sizes (the N 's) the number of slots, NS, and the standard values of the property (the Δ's), we find the threshold value, Δ, by solving (B.2) numerically. The standard value (Δ) for the reference group is zero. Knowledge of it allows evaluation of each term, giving the number selected from each group. Another form of (B.2) is convenient for processing data given as percentages of a population. The high-school student suspension data were given in this form. Multiplying (B.2) thru by 100/ΣNi gives
where pi is the percentage of the population made up by group i, and pS is the percentage of the population occupying slots. For the suspended-student problem there are two terms in (B.3), one for whites and one for blacks. Taking whites as the reference group, and using the value 0.37 SD obtained from Table 1 for the black Standard Aggressiveness, λ may be found by numerical solution of (B.3), followed by evaluation of the individual terms on the left of (B.3). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||