Affirmative action is not free. No matter how large or small a business is, it is vulnerable to complaints of discrimination by applicants, employees and former employees. In the interest of the bottom line, employers invariably capitulate. The consequences of not conforming are more costly. Brimelow and Spencer in When Quotas Replace Merit, Everybody Suffers, Forbes, February 15, 1993, assert that the greatest cost of affirmative action results from not being able to choose the best economic alternatives. They estimate this cost alone at $236 billion for 1991. Administrative costs associated with affirmative action add another $100 billion or so per year. Most other estimates also put the annual bill for affirmative action in the two to four hundred-billion dollar ballpark. 

The Robin Hood Effect 
   There is another cost of affirmative action, the most insidious and cruel of all. Different from the others, we cannot measure it as reduced GDP. It is a tax on one group to reward another. The concept is not abstract. It is well-known to people in the workplace when they see less qualified minorities steal away their opportunities. Resentment is often palpable, and the cost is psychological as well as economic. We address the economic component here. 

   Whenever someone gets preferential access to a job or a promotion because of his race or ethnicity, someone else of a different race or ethnicity gets displaced. In the U.S., the displaced person is usually a non-Hispanic white. The result is an income transfer from whites to "preferred" minorities. We call it the Robin Hood effect. We have assessed its size by using a simple device: the correlation of income and IQ. From this relation we can construct a profile of the workforce as it would exist in a meritocracy,

The Income-IQ Nexus 
   Income-IQ correlation is well documented. Recently, the link has been forged conclusively. (See for example, Charles Murray, 1998. Income Inequality and IQ, AEI Press.) The connection, however, is not perfect. Various factors contribute to produce fluctuations in the IQ-income curve. There is, for example, variation in human drive or ambition. We might not expect someone with an IQ of 120 to be a clerk, but he might not push himself hard enough to be, say, a dentist. Also, income does not always govern our job choices. We might surmise that professors at research universities are as a group more intelligent than dentists. Dentists, however, generally earn more. If research did not pay a decent wage, then many professors might also choose to make a living poking about in the mouths of strangers. But since professors and dentists both earn well, room is left for other considerations. 

   Then there is luck. A person must be available when an opportunity pops up. Geography may be a factor. New Yorkers have more opportunity to earn well than West Virginians. Sometimes, ties to family and geography will constrain people from seeking or taking the best jobs. Lastly, other qualities like personality, work habits, ethical or moral values, to name a few, factor into the ability to earn. All these and more produce fluctuations in the income-IQ curve, a problem we need to solve. 

   By dividing the workforce into broad ranges, say quintiles, we can virtually eliminate the fluctuations. Each quintile will contain millions of earners. Dentists and professors, with rather different incomes, will fall into the same income quintile. If IQ correlates well with income, it will correlate almost perfectly with the income of a work force so partitioned. 
 
Income Distributions
We ask three questions:

1) What would income distribution by race and ethnicity look like in Utopia? 

2) What would income distribution by race and ethnicity look like in a meritocracy? 

3) What is the actual income distribution by race and ethnicity in the U.S.? 

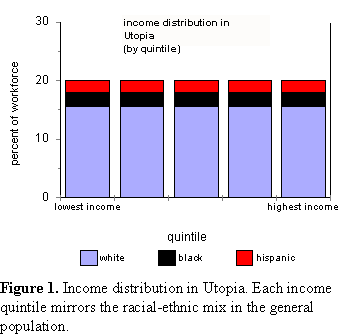   The Utopian justification of affirmative action is illustrated by the testimony of Representative Sheila Jackson Lee before the Subcommittee on the Constitution, Committee on the Judiciary, U.S. House of Representatives, December 7, 1995. Speaking of women, roughly 50 percent of the population, she argued:

"As long as women make up only 8 percent of engineers, 31 percent of scientists, and 16 percent of physicists, we have much work ahead of us." 

Meritocratic distribution. The IQ-income nexus allows us to estimate the income distribution in a meritocracy. First divide the labor force into quintiles according to income. Imagine the quintiles to be boxes. Each box holds 20 percent of the workforce. From the pool of all earners, find the most intelligent and throw him into the highest income box. Locate the next smartest worker and throw him in for company. Proceed down the line, each time choosing the most intelligent of those left, until the highest-income box is filled. Then fill the next highest-income box in the same way. When it is filled, go to the next box and so on until all five boxes are filled. In the end the highest IQ workers will populate the highest-income quintile, and so on down the line. 

   To generate the rank ordering of the workforce on IQ, required to construct the meritocratic distribution, we used mean IQ differences from the National Longitudinal Study of Youth (NLSY): 1.21 SD for the white-black difference, and 0.93 SD for the white-Hispanic difference. The mathematical procedure for populating the quintiles is described in an Appendix. 

Actual distribution. The U.S. Government compiles impressive amounts of social data. Virtually every social statistic is recorded somewhere in its archives. We used data from the Annual Demographic Survey (ADS) to construct the quintile distribution. The survey is jointly sponsored by the Bureau of Labor Statistics and the Bureau of the Census. It tabulates income by race, ethnicity, sex and age. We used ADS data of 1997. 

   The ADS classifies workers as black, white, Hispanic, and white-not-Hispanic. Since Hispanics can be of any race, we formed the classification Hispanic-white by subtracting the white-not-Hispanic data from the white data. Ultimately, we formed three non-overlapping groups: black, Hispanic-white, and non-Hispanic white.  For simplicity, from now on we refer to these groups as black, Hispanic and white, respectively. All but a few percent of Americans who earned income in 1997 were included in our analysis. (The ADS data of 1997 did not include Asian Americans.) 

   Income in the ADS is broken into $2,500 bins: $0 to $2,499, $2,500 to $4,999, and so on through $97,500 to $99,999. Finally, the last bin is for earners making $100,000 or more. The ADS breaks down the population of each bin by race, ethnicity, sex and age. We included in our sample only workers between the ages of 25 and 64, the mainstream of full-timers. They numbered 126,362,000 in 1997. 

   Starting at the low-income end, we added earners in adjacent bins until we got as close as possible to 20 percent of the workforce. In this way we partitioned the workforce into near-quintiles, each containing 20±1 percent of all workers. By using near-quintiles instead of true quintiles, we sacrificed nothing but symmetry. Near-quintiles flatten the fluctuations as well as true quintiles. Table 1 summarizes the partition. 
 
 

(Near) Quintile	No. of workers (1,000s)	% of all workers in quintile	No. of whites in quintile (1,000s)	No. of blacks in quintile (1,000s)	No. of Hispanics in quintile (1,000s)	% of whites in quintile	% of blacks in quintile	% of Hispanics in quintile
$0- $9,999	25,504	20.2	18,328	3,853	3,323	18.6	25.0	27.4
$10,000- $19,999	25,906	20.5	18,114	3,979	3,813	18.3	25.8	31.4
$20,000- $29,999	23,899	18.9	18,400	3,262	2,237	18.6	21.1	18.4
$30,000- $44,999	24,900	19.7	20,595	2,641	1,664	20.9	17.1	13.7
$45,000 and over	26,153	20.7	23,345	1,693	1,115	23.6	11.0	9.2
totals	126,362	100.0	98,782	15,428	12,152	100.0	100.0	100.0
Table 1.   Partition of the workforce into near-quintiles

 

Results 
   Table 2 compares, for each racial/ethnic group, actual and meritocratic distributions of income. Table 3 does the same but uses percentages rather than numbers of workers. 
 

(Near)   Quintile	All  earners	Whites  (actual)	Blacks  (actual)	Hispanics  (actual)	Whites  (meritocratic)	Blacks   (meritocratic)	Hispanics   (meritocratic)
$1 - $9,999	25,504	18,328	3,853	3,323	12,386	8,093	5,025
$10,000 -$19,999	25,906	18,114	3,979	3,813	18,957	3,768	3,182
$20,000 -$29,999	23,899	18,400	3,262	2,237	19,981	1,963	1,955
$30,000 -$44,999	24,900	20,595	2,641	1,664	22,448	1,135	1,317
$45,000   and over	26,153	23,345	1,693	1,115	25,010	470	673
totals	126,362	98,782	15,428	12,152	98,782	15,429	12,152
Table 2.   Income distribution in a meritocracy compared with the actual distribution. The numbers are in 1000s of workers. (Sums may not agree perfectly due to roundoff.)

 
 

(Near)   Quintile	All   earners	Whites   (actual)	Blacks   (actual)	Hispanics   (actual)	Whites   (meritocratic)	Blacks   (meritocratic)	Hispanics   (meritocratic)
$1 - $9,999	20.18	18.55	24.97	27.35	12.54	52.46	41.35
$10,000 -$19,999	20.50	18.34	25.79	31.38	19.19	24.42	26.18
$20,000 -$29,999	18.91	18.63	21.14	18.41	20.23	12.72	16.09
$30,000 -$44,999	19.71	20.85	17.12	13.69	22.72	7.36	10.84
$45,000   and over	20.70	23.63	10.97	9.18	25.32	3.04	5.54
totals	100.00	100.00	99.99	100.01	100.00	100.00	100.00
Table 3.   Income distribution in a meritocracy compared with the actual distribution. The numbers are the percentages of each group. (Sums may not agree perfectly due to roundoff.)

 

Analysis 
The case for affirmative action.  In Utopia, 20 percent of each group would fall in each earning quintile. By this criterion, blacks and Hispanics do poorly. Only 11.0 percent of blacks and 9.2 percent of Hispanics are in the highest-income bracket. The lowest income bracket, however, is overpopulated with blacks and Hispanics; 25.0 percent of blacks and 27.4 percent of Hispanics fall there. Figure 2 illustrates for blacks these inequities measured against Utopian expectations. 
 
 

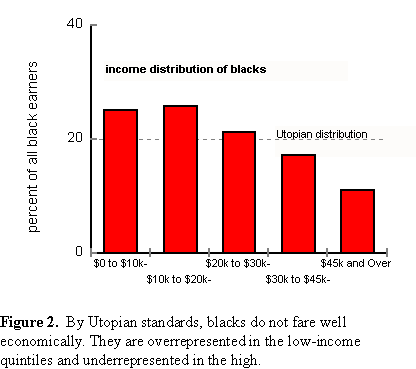   Figure 3 shows how blacks would fare in a meritocracy, where a very different picture emerges. 
 

   Comparison of Figures 2 and 3 shows that blacks have gained enormously under affirmative action. The eccentricities of their income distribution have been compressed toward the Utopian ideal. The effect is dramatic. Left to a free market, more than half (52.5 percent) of black full-time workers would have earned less than $10,000 in 1997, not surprising for a group with half its members under 85 IQ. Remarkably, affirmative action reduced the number of blacks in this lowest-income quintile to less than 25 percent. Similar, but somewhat less dramatic gains have been made by Hispanics. In a free market, about 41 percent of Hispanics would be in the $0 to $9,999 bracket. Affirmative action has reduced this to about 27 percent. 

   Too good to be true? That depends on your philosophical perspective. This is a zero-sum game. To reduce black and Hispanic representation in low-income brackets and increase it in high-income brackets, whites must be displaced. 

The size of the Robin Hood effect. The income lost to whites is easily assessed. The number of whites displaced into or out of a given quintile is the difference between the white quintile population in a meritocracy and that actually observed. The number of displaced whites times the midpoint income of a quintile approximates the lost income for that quintile. The total income lost is the sum of losses over the 5 quintiles. Table 4 illustrates the calculation. 
 

(near) quintile	(1)   number of whites   (actual)	(2)   number of whites   ( if meritocracy)	(2) - (1)	income lost by whites*
$1 - $9,999	18,328,000	12,386,000	(5,942,000)	($29,710,000,000)**
$10,000 -$19,999	18,114,000	18,957,000	843,000	$12,645,000,000
$20,000 -$29,999	18,400,000	19,981,000	1,581,000	$39,525,000,000
$30,000 -$44,999	20,595,000	22,448,000	1,853,000	$69,487,500,000
$45,000   and over	23,345,000	25,010,000	1,665,000	$99,900,000,000
totals	98,782,000	98,782,000	0	$191,847,500,000
Table 4.   Calculation of income lost by whites because of affirmative action. In a quintile, the income lost by whites is approximately the difference between the white population of the quintile in a meritocracy and the actual white population, times the midpoint income in the quintile. The sum of these quantities is the net lost income, about $192 billion.  * For the $45,000 and over bracket, the midpoint was taken as $60,000.  ** The apparent income gain in the $1 - $9,999 quintile is an artifact caused by whites being displaced into this bracket from higher brackets. See the Cascade Effect below.

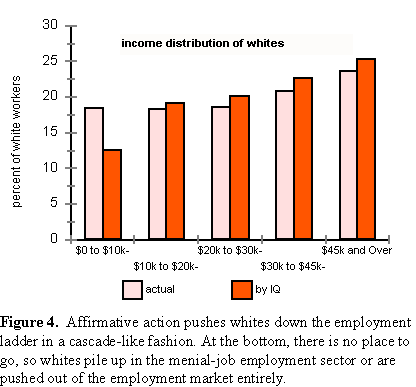
   In 1997, because of affirmative action, about $192 billion in income was transferred from whites to preferred minorities. If we perform precisely the same calculation for blacks and Hispanics, we can break down the $192 billion into the amounts gained by each group. We find that $144.3 billion was transferred to blacks and $47.5 billion to Hispanics. Dividing these gains by the respective numbers of black and Hispanic workers, we can compute their average annual income enhancement. In 1997, on average a black was subsidized to the tune of about $9,400; a Hispanic gained an average of about $3,900. The cost of these subsidies was spread over 98,782,000 white workers who suffered an average loss of about $1,900 to pay the bill. 

The cascade effect. The net displacement of whites by minorities is not uniformly spread across the quintiles. When high-earning whites are displaced down the employment ladder, they displace other whites downward by exerting pressure on the rung below. The effect is like a cascade. At the bottom there is no rung left. Low IQ whites, who in an affirmative action-free marketplace would be competitive in the $10,000 to $20,000 bracket, now pile up in the lowest-income quintile. Although affirmative action affects every white, the largest number affected are the least intelligent and competitive. Figure 4 illustrates the cascade effect. 
 
 

Summary 
   Decades of affirmative action have brought enormous changes to the American workforce. Blacks and Hispanics have gained generously, but at the expense of whites. The costs of these gains have been borne by the majority white population. To some extent the costs are masked by the relative sizes of the white and minority groups. Large numbers of whites foot the bill for relatively few minority workers. Thus, individual minority workers can achieve large earning enhancements, with the cost to whites spread over a large population. A philosophical case could be made for affirmative action in this way. Such an argument, however, is unlikely to surface while the Utopian mindset prevails. In the current political climate, we have nothing to look forward to but an asymptotic approach to Utopia. 
 

APPENDIX.  Rank Order Filling of n-tiles 

   Suppose we wish to fill N_S slots in rank order on some property, x, from a population that consists of M groups. Let the ith group contain N_i members. Choose one group as the reference group, with a normalized distribution of the property, P(x). Let the distribution function of the ith group differ from P(x) by a translation, Δ_i, along the property axis. 

   In Women and Minorities in Science, we showed that under these assumptions the following relation is satisfied. 
 

   Members of the population possessing a value of the property greater than or equal to λ make the cutoff and fill one of the slots. The value of λ is determined in practice by numerical solution of (1). 

   For the case of filling successive n-tiles from the top down by rank order on the selected property, we can use a generalization of (1):
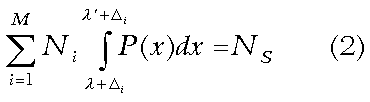